

摘要:協同自適應巡航控制(CACC)系統中車輛縱向運動的上下位分層控制器結構,上位控制器采用狀態空間模型預測控制算法,利用期望距離以及車輛與環境的實時信息決策出被控車輛運動的期望加速度。下位控制器根據期望加速度,求解發動機節氣門開度或制動壓力。車輛的執行器時延會對系統的穩定性產生很大的影響。根據動態矩陣控制算法對純滯后對象的補償作用,本文提出一種改進的模型預測控制算法,并與PID 控制算法(下位控制器)相結合形成自主車輛縱向運動的上下位分層控制器,以補償車輛的執行器時延帶來的影響。通過 SIMULINK/CARSIM 聯合仿真平臺對所設計的算法進行了仿真研究,仿真結果表明所設計算法減小了 CACC 系統車輛在跟隨過程中的速度跟蹤誤差以及間距誤差,提高了系統的穩定性法。
1.引言
為了解決因汽車保有量增加而帶來的社會問題,大量的駕駛員輔助控制系統被深入研究并取得了一定的運用效果[1-2]。比如車道偏離預警系統(lanedeparture warningsystem,LDW)、車道保持輔助系統(land keeping assistance system,LKA)、行人檢測和回避系統,交通路口避撞系統和停車輔助系統等。協同自適應巡航控制(CACC)系統以 ACC系統為基礎,引入無線通信技術進行車間信息交互并將通信信息用于車輛控制,由此獲得比 ACC 系統更好的控制效果,大大提高了自主駕駛的安全性與舒適性[3]。CACC研究主要涉及自適應巡航控制、車間通信技術及控制算法三方面。
2000年,Stankovi等設計了一種基于分布式的重疊控制算法,并對車隊的穩定性條件進行相應的分析[4]。2008年,卡內基梅隆大學研究團隊構建了油門和制動的非線性 PID控制策略,并設計了基于速度偏差的油門/制動的切換邏輯,進而應用于 Boss 智能車獲得了 DARPA挑戰賽的冠軍[5]。2011年, 郭戈等人對協同駕駛系統進行了分層控制,使系統獲得一個較優的控制性能[6]。2012 年,Iftekhar為車輛正常行駛、換道和剎車這三種不同的駕駛狀態設定了邏輯切換條件,并設計了協同駕駛控制算法, 從而實現復雜城市道路環境中的協同駕駛[7]。2013年, 以減少燃油損耗為協同控制目標,Stanger重新構建了自主車輛的 MPC優化目標函數[8]。2015 年, Kim 在韓國首爾大學研究室建立了具有集總參數特征的車輛縱向線性模型,進而設計了一種參數時變自適應速度控制器并進行了仿真實驗[9]。但是,上述文獻忽略了 CACC 車輛執行器的時延,這會降低跟蹤的平滑性,甚至使系統發散[10]。
本文首先建立了協同車輛系統的狀態空間模型,針對執行器延時,對傳統模型預測控制算法(MPC) 進行改進, 以此設計上位控制器。另將CARSIM 中的車輛作為復雜車輛模型以設計下位控制器,二者相結合形成上下位分層結構控制的CACC 系統,并于 CARSIM/SIMULINK 聯合仿真平臺上進行數值仿真實驗。
2.CACC 系統建模
本文采用經典的上下位分層控制結構[11],上位控制器通過期望距離以及車輛與環境的實時狀態信息決策出控制車輛行為的期望加速度;下位控制器根據期望加速度,求解發動機節氣門開度和制動壓力。
2.1 自主車輛的運動學方程描述
自主車輛縱向運動過程由以下微分方程描述:
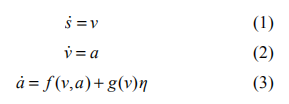
其中 s 為自主車輛相對于慣性參考點的縱向位置, v, a 分別為車輛的速度和加速度,η為發動機的控制輸入。函數f 和 g 分別為:

上兩式中, Cd 代表了氣動阻力系數, m 為車輛的質量, t為車輛發動機的時間常數, dm 為車輛的機械阻力。
將式(4)與(5)中各參數視為先驗已知,則可采用下式中的控制律對原非線性模型反饋線性化:
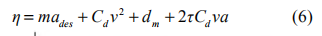
其中 ades 為上位控制器所決定的期望加速度。將式(4)~(6)代入式(3),可得線性化方程:

上式也可寫為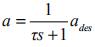 ,表明發動機跟蹤特性可用一階滯后建模,即實際加速度a 以時間常數τ跟蹤期望加速度 ades 。
,表明發動機跟蹤特性可用一階滯后建模,即實際加速度a 以時間常數τ跟蹤期望加速度 ades 。
2.2 CACC車隊系統狀態空間模型
如圖 1,考慮直道上的行駛車隊:
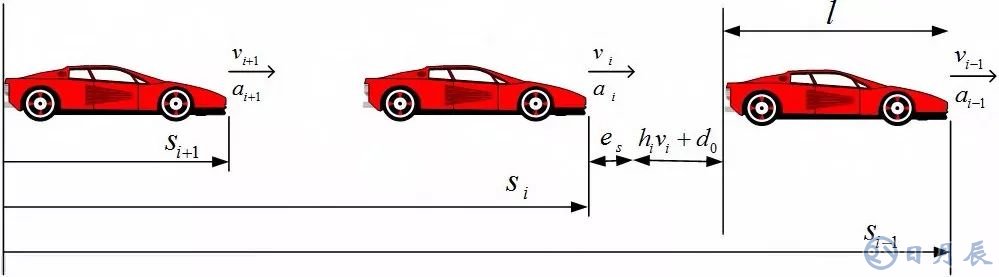
圖 1 協同自適應巡航控制車隊
其中 si 代表第i 輛車與慣性參考點的距離,vi 、 ai 分別代表第i 輛車的速度和加速度, l 代表車身的長度,則第 i 輛車與前車的車間間距誤差為:

其中 di,des 是第i 輛車距前車的期望車間距離,本文采用固定車頭時距策略,有:

其中 d0 表示靜止時最小安全距離, h 為常數。此外,定義速度差為:

根據式(2)、(7)~(10),可以推導出 CACC 系統內車輛的狀態空間模型為:
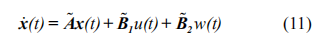
此處
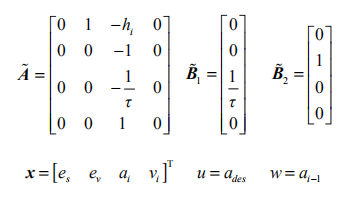
其中x、u和w分別為狀態矢量、控制輸入以及干擾。
3.上位控制器設計
這部分分析線性狀態空間模型中MPC 算法的應用,并在求解有約束的最優化問題時引入松弛變量,在此基礎上,針對有執行器時延的系統,提出改進 MPC算法。
3.1 線性狀態空間 MPC算法
考慮以下離散狀態空間模型:
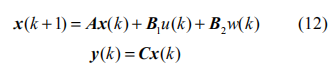
其中 表示系統狀態向量,
表示系統狀態向量,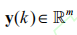 表示系統輸出,
表示系統輸出,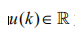 為系統控制輸入,而 w(k) 為前車加速度, C = [1, 0, 0, 0; 0,1, 0, 0] 為輸出矩陣。
為系統控制輸入,而 w(k) 為前車加速度, C = [1, 0, 0, 0; 0,1, 0, 0] 為輸出矩陣。
假設每個采樣周期ts的狀態和干擾可測,通過迭代計算,記 x(k + j | k) 為系統在 k 時刻對 k + j 時刻的狀態預測,以u(k |k) 代表預測的控制輸入,控制過程通過增量控制Δu 實現:
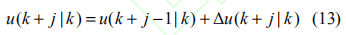
則可得到總的模型預測狀態方程為:

其中參數矩陣Φ,Γ,F,G 見[12],k時刻的預測控制輸出為:
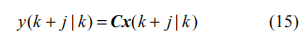
定義性能指標函數:
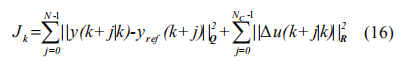
其中 yref 為參考軌跡,N 為預測時域,NC 為控制時域。Q, R 分別為誤差和輸入加權矩陣。
優化函數的向量形式為:

其中
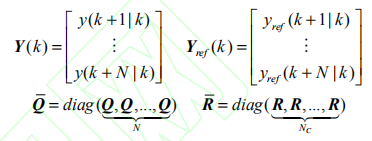
定義向量 E(k) 為系統自由響應與未來目標軌跡的偏差:
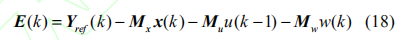
其中
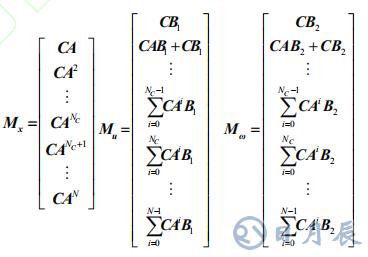
將(18)式代入(17)可得:
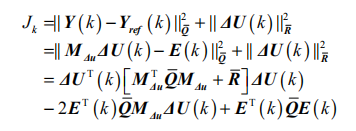
上式可被寫為二次規劃的標準形式:

其中
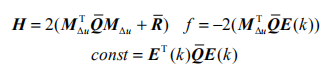
其中, MΔu 為 Γ 中每個分塊矩陣左乘C 。
假設優化函數受到如下的逐點約束條件:
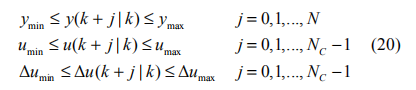
上式對應的向量形式為:

其中

I 為 P 維單位矩陣,其中參數矩陣ΔUmax ,ΔUmin ,Umax,U min 見[11],Π 為 PNC 維單位矩陣。
3.2 引入松弛變量
求解有約束最優化問題時,過于嚴格的約束可能得不到可行解,需引入松弛變量作為罰函數加入原目標函數,得到新的優化函數:
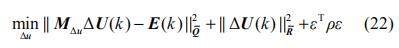
此處 ε 為松弛變量而 ρ 為其權重。新的約束條件為:

3.3 考慮執行器延時的改進 MPC 算法
由于Δu (k ) 是極小化性能指標得到的解,則必須滿足極值必要條件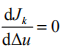 ,可得式(22)的解:
,可得式(22)的解:
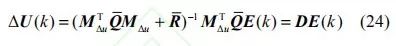
k 時刻的實際增量控制輸入為:
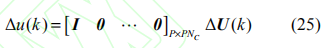
對執行器時延系統,基于動態矩陣控制思想改進傳統 MPC 算法。將增量控制輸入視為階躍輸入,則執行器時延對應系統階躍響應系數的時延,進而轉換為控制輸入的時延。故執行器時延為θ 的系統相當于具有純滯后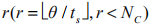 拍的離散模型其增量控制輸入表示為:
拍的離散模型其增量控制輸入表示為:
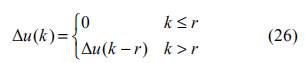
對應的優化參數變為:

由改進算法求得的控制輸入為:
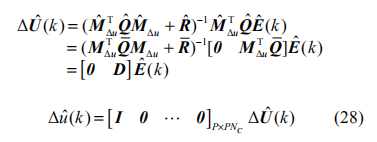
以上分析說明,對于執行器時延系統,在傳統MPC 控制器基礎上,將參數按式(27)進行修改,并以Δu(k-r) 作為 k 時刻的增量控制輸入即可。
4.下位控制器設計
實際車輛在行駛的過程中,加速控制和制動控制分開執行,可根據期望加速度大小進行邏輯切換,當 ades ≥ 0 時,采用加速控制,當 ades<0 時,采用制動控制。
4.1 逆動力學模型
圖 2 為不同油門開度下發動機轉速與扭矩的關系曲線,其中每條曲線旁邊的數字對應油門開度。
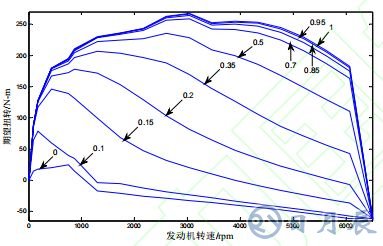
圖 2 逆動力學發動機扭矩特性曲線
若已知發動機轉速 we 和期望扭矩Te,des ,便可通過查表法得到對應的期望油門開度αdes ,即:
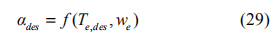
4.2 加速控制
自主車輛縱向行駛是汽車牽引力、風阻力與地面阻力共同作用的結果,行駛狀態與車輛的具體模型、道路的光滑程度以及風阻力系數的大小等息息相關。縱向行駛過程中的等效空氣阻力為:

其中 ρa 為空氣質量密度,Cd 為空氣阻力系數,AF 為車輛的正面迎風面積,Vx 和Vwind 分別為車輛的縱向速度以及風速。
空氣阻力 Faero 是車輛速度的二次函數,可表示為發動機轉速 we 的二次函數:
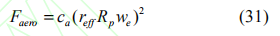
由式(30),有
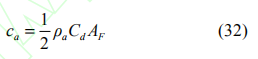
Rp 為車輪轉速 ww 與發動機轉速 we 之間的比值,即變速齒輪比。 reff 為輪胎有效半徑。
加速過程中,發動機期望扭矩Te des , 與期望加速度之間的關系為:
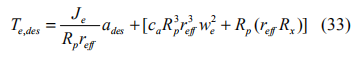
式中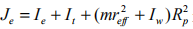 是反映在發動機側的有效轉動慣量, Ie 為發動機轉動慣量,m 為汽車質量。Rx 為所有滾動阻力之和,與滾動阻尼系數 f 有關,因為 f 一般取值為0.01-0.04,故 Rx 值很小,本文予以忽略。由于
是反映在發動機側的有效轉動慣量, Ie 為發動機轉動慣量,m 為汽車質量。Rx 為所有滾動阻力之和,與滾動阻尼系數 f 有關,因為 f 一般取值為0.01-0.04,故 Rx 值很小,本文予以忽略。由于
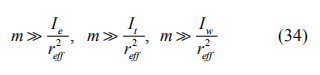
則Je 可改寫為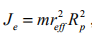 ,式(32)重寫為:
,式(32)重寫為:

本文研究對象為前輪驅動式的 B 型掀背式轎車,由逆動力學關系得到相應的期望油門開度αdes ,采用 PID 算法對誤差進行校正,最終油門輸入為:
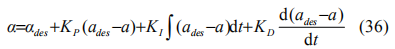
測試后設定參數為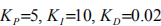 。
。
4.3 制動控制
汽車制動時,根據期望加速度求出期望制動壓力。制動過程時車輛動力學方程為:
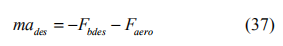
在制動力不超過路面所能達到的最大制動力的情況下,可以將制動力 Fbdes 與制動壓力 Pbdes 視為線性關系:

CARSIM 仿真可得 Kb = 1286.174。
由式(36)與式(37)可得期望制動壓力為:

采用與加速控制時相同的 PID 控制器進行校正,得到最終的制動壓力為:
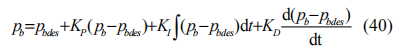
5.CARSIM/SIMULINK 聯合仿真
CARSIM 提供了與 SIMULINK 聯合仿真的接口,通過 S 函數實現通信。聯合仿真實驗采用的CARSIM 車輛均為前輪驅動式的 B 型轎車,發動機功率為 125kW,仿真環境為長 1200m 的單行道。車輛在 CARSIM 中設置為“AT 4th Mode”運動模式,即車輛自動駕駛在 4 檔及 4 檔以下,根據發動機轉速自動選擇傳動比。自動切換轉速曲線如圖 3 所示:
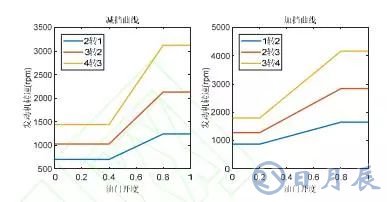
圖 3 加減檔下油門門開度與發動機轉速曲線
車輛運行在 1 檔時傳動比為 0.28,在 2 檔時0.485, 在 3 檔時 0.71,在 4 檔時為 1.00。
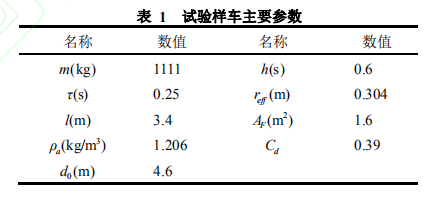
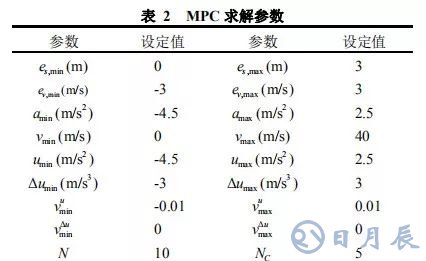
實驗樣車各參數如表 1 所示:
約束參數、松弛變量和控制器優化參數設為:

聯合仿真模型如下:
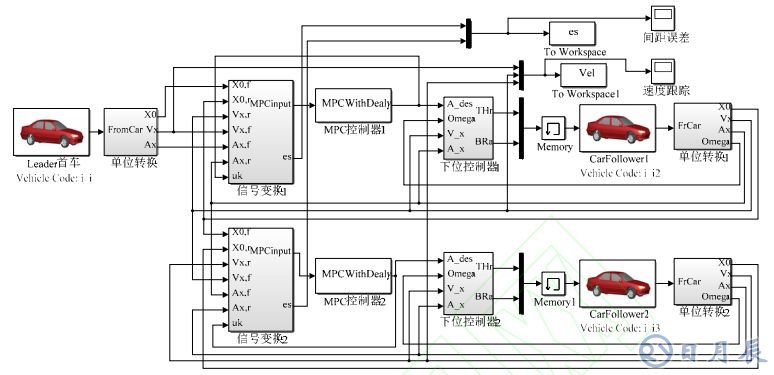
圖 4 上下分層控制系統仿真模型
執行器延時為 0.2s,采樣周期 0.1s,基于上下位分層控制的 CACC 系統進行建模仿真。三輛車的初始位置分別為 20m、12m 和 4m,初始速度與加
速度都為 0。首車速度曲線如圖 5 a)中的 V1所示。
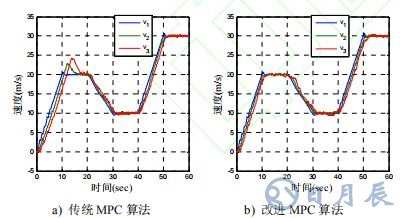
圖 5 兩種算法下 CACC 系統車輛的速度曲線
由圖 5 可知,采用傳統 MPC 算法的自主車輛雖然能跟蹤上前車的速度,但跟蹤過程中出現超速和較大抖動,可能導致車隊的不穩定。而采用改進MPC 算法時后面車輛沒有超速行為,跟蹤曲線相對平滑,隊列運行穩定,驗證了改進算法的有效性。

圖 6 兩種算法下 CACC 系統車輛間間距誤差
圖 6 中 ,es,1-2,es2-3分別代表首車與第二輛車,第二輛車與第三輛車之間的間距誤差。對比可知,傳統 MPC 算法下車輛間距超過了約束限制,間距過長會導致無法保持緊密隊形,違背 CACC 系統保持較小間距以增大道路交通容量的設計初衷。改進MPC 算法可將車輛間距誤差保持在 1.5m 以內,是傳統方法的 18.7%,驗證了改進算法的有效性。
當執行器時延為 0.4s 時,車輛跟蹤性能下降,第二輛車和首車的最大間距誤差達到 2.5m,第三輛車與第二輛車的間距誤差則最高達到 3.96m,相比時延為 0.2s 時變差;時延為 0.4s 時傳統 MPC 算法無法保證系統的穩定性。執行器時延為 0.1s 時,速度跟蹤比較平滑,間距誤差也控制在 1.2m 以內。改進后的算法在執行器時延存在的情況下仍能實現車輛跟蹤,但隨著時延增大,系統性能指標有所下降。
6.結束語
本文針對車輛的執行器時延,基于動態矩陣方法改進了傳統 CACC 模型預測控制算法。在每個采樣時刻,上位控制器將控制量求解問題轉化為一個二次型優化問題,得到車輛期望加速度,再根據車輛逆縱向動力學模型設計 PID 下位控制器,二者相結合組成分層控制結構,實現對復雜車輛模型的協同控制。CARSIM/SIMULINK 聯合仿真驗證了改進算法有效性。